链表-判断链表是否包含环

发表于 分类于

判断链表是否包含环属于经典问题了，解决方案也是用快慢指针。

每当慢指针 slow 前进一步，快指针 fast 就前进两步。

如果 fast 最终遇到空指针，说明链表中没有环；如果 fast 最终和 slow 相遇，那肯定是 fast 超过了 slow 一圈，说明链表中含有环。

只需要把寻找链表中点的代码稍加修改就行了。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
/**
 * 判断链表是否包含环
 * @param head
 * @return
 */
public static boolean hasCycle(ListNode head) {
    //快慢指针初始化指向head
    ListNode slow = head, fast = head;
    //快指针走到末尾时停止
    while (fast!=null && fast.next!=null){
        //慢指针走一步，快指针走两步
        slow = slow.next;
        fast = fast.next.next;
        //快慢指针相遇，说明含有环
        if(slow==fast){
            return true;
        }
    }
    //不包含环
    return false;
}

当然，这个问题还有进阶版：如果链表中含有环，如何计算这个环的起点？

这里简单提一下解法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
/**
 * 如果链表包含环，计算这个环的起点
 * @param head
 * @return
 */
public static ListNode detectCycle(ListNode head) {
    ListNode slow = head, fast = head;
    while (fast!=null && fast.next!=null){
        slow = slow.next;
        fast = fast.next.next;
        if(slow == fast)
            break;
    }
    if(fast == null || fast.next == null ){
        //fast遇到空指针，说明没有环
        return null;
    }
    //重新指向头结点
    slow = head;
    //快慢指针同步前进，相交点就是环起点
    while (slow!=fast){
        slow = slow.next;
        fast = fast.next;
    }
    return slow;
}

可以看到，当快慢指针相遇时，让其中任一个指针指向头节点，然后让它俩以相同速度前进，再次相遇时所在的节点位置就是环开始的位置。

为什么要这样呢？这里简单说一下其中的原理。

我们假设快慢指针相遇时，慢指针 slow 走了 k 步，那么快指针 fast 一定走了 2k 步：

img

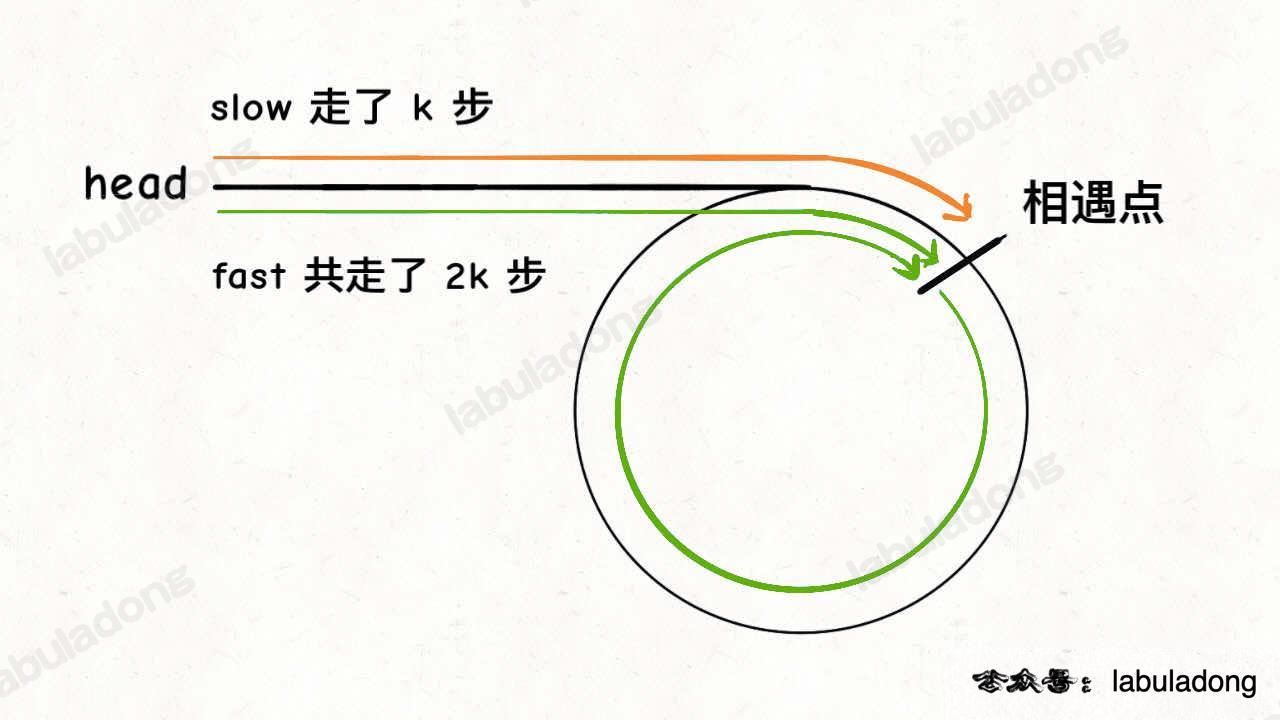
fast 一定比 slow 多走了 k 步，这多走的 k 步其实就是 fast 指针在环里转圈圈，所以 k 的值就是环长度的「整数倍」。

假设相遇点距环的起点的距离为 m，那么结合上图的 slow 指针，环的起点距头结点 head 的距离为 k - m，也就是说如果从 head 前进 k - m 步就能到达环起点。

巧的是，如果从相遇点继续前进 k - m 步，也恰好到达环起点。因为结合上图的 fast 指针，从相遇点开始走k步可以转回到相遇点，那走 k - m 步肯定就走到环起点了：

img

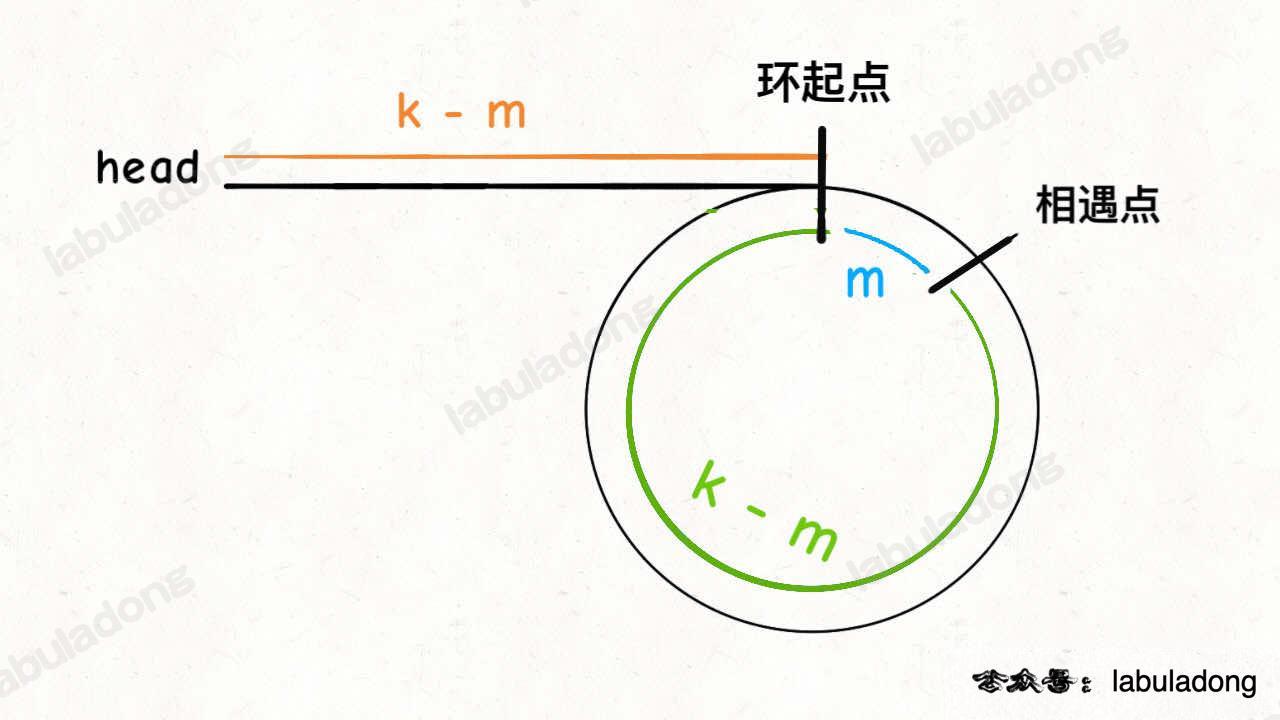
所以，只要我们把快慢指针中的任一个重新指向 head，然后两个指针同速前进，k - m 步后一定会相遇，相遇之处就是环的起点了。