C++实现贪心算法

贪心算法（又称贪婪算法）是指，在对问题求解时，总是做出在当前看来是最好的选择。也就是说，不从整体最优上加以考虑，他所做出的仅是在某种意义上的局部最优解

贪心算法思想

1.贪心算法（又称贪婪算法）是指，在对问题求解时，总是做出在当前看来是最好的选择。也就是说，不从整体最优上加以考虑，他所做出的是在某种意义上的局部最优解。
2.贪心选择是指所求问题的整体最优解可以通过一系列局部最优的选择，即贪心选择来达到。这是贪心算法可行的第一个基本要素。
3.当一个问题的最优解包含其子问题的最优解时，称此问题具有最优子结构性质。运用贪心策略在每一次转化时都取得了最优解。问题的最优子结构性质是该问题可用贪心算法求解的关键特征。贪心算法的每一次操作都对结果产生直接影响。贪心算法对每个子问题的解决方案都做出选择，不能回退。
4.贪心算法的基本思路是从问题的某一个初始解出发一步一步地进行，根据某个优化测度，每一步都要确保能获得局部最优解。每一步只考虑一个数据，他的选取应该满足局部优化的条件。若下一个数据和部分最优解连在一起不再是可行解时，就不把该数据添加到部分解中，直到把所有数据枚举完，或者不能再添加算法停止。
5.实际上，贪心算法适用的情贪心算法(贪婪算法)况很少。一般对一个问题分析是否适用于贪心算法，可以先选择该问题下的几个实际数据进行分析，就可以做出判断。

该算法存在的问题
1.不能保证求得的最后解是最佳的
2.不能用来求最大值或最小值的问题
3.只能求满足某些约束条件的可行解的范围

贪心算法的应用

选择排序、平衡字符串、买股票最佳时机、无重叠区间

下文将分别展示这几种的应用。

选择排序

我们熟知的选择排序，其采用的就是贪心策略。 它所采用的贪心策略即为每次从未排序的数据中选取最小值，并把最小值放在未排序数据的起始位置，直到未排序的数据为0，则结束排序。

void swap(int *arr, int i, int j){
    int temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}

void selectSort(int *arr, int n){
    for(int i=0;i<n;i++){
        int minIndex = i;
        for(int j=i+1;j<n;j++){
            if(arr[j] < arr[minIndex])
                minIndex = j;
        }
        swap(arr, minIndex, i);
    }
}

平衡字符串

问题描述：
在一个 平衡字符串 中，‘L’ 和 ‘R’ 字符的数量是相同的。
给你一个平衡字符串 s，请你将它分割成尽可能多的平衡字符串。
注意：分割得到的每个字符串都必须是平衡字符串，且分割得到的平衡字符串是原平衡字符串的连续子串。
返回可以通过分割得到的平衡字符串的 最大数量 。

输入：s = “RLLLLRRRLR”
输出：3
解释：s 可以分割为 “RL”、”LLLRRR”、”LR” ，每个子字符串中都包含相同数量的 ‘L’ 和 ‘R’ 。
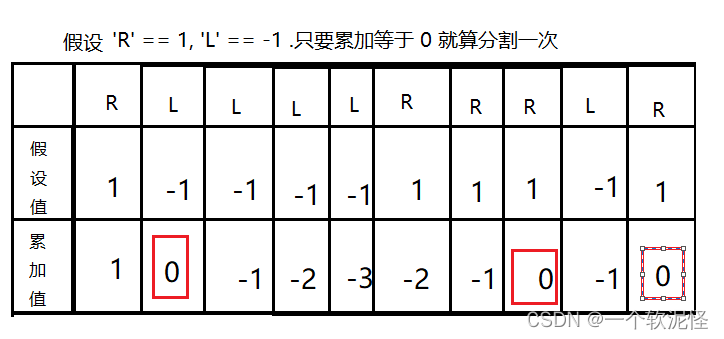
解题思路: 不要有嵌套的平衡，只要达到平衡，就立即分割(贪心策略).我们假设 ‘R’ == 1, ‘L’ == -1 .只要累加等于 0 就算分割一次.

int balancedStringSplit(const string& s) {
    if(s.size() == 1)
        return 0;
    int cnt = 0;
    int balance = 0;
    for(char i : s){
        if(i == 'R')
            --balance;
        else
            ++balance;
        if(balance == 0)
            cnt++;
    }
    if(cnt == 0)
        return 1;
    return cnt;
}

买股票最佳时机

问题描述：
给定一个数组 prices ，其中 prices[i] 是一支给定股票第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易（多次买卖一支股票）。
注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。
贪心策略：
连续上涨交易日：第一天买最后一天卖收益最大，等价于每天都买卖。
连续下降交易日：不买卖收益最大，即不会亏钱。
故可以遍历整个股票交易日价格列表，在所有上涨交易日都买卖（赚到所有利润），所有下降交易日都不买卖（永不亏钱）

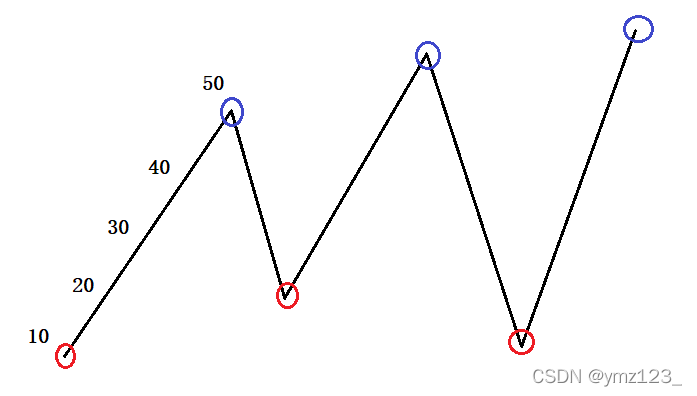
例如从10到50是连续上涨的5天，可以第一天买入，最后一天卖出，利润为40，等价于第一天买入第二天卖出，第二天再买入。。。以此类推

代码实现：

int maxProfit(vector<int>& prices) {
	int profit = 0;
	for(int i = 0; i < prices.size() - 1; i++)
	{
		if(prices[i] <= prices[i+1])
			profit += prices[i+1] - prices[i];
	}

	return profit;
}

无重叠区间

问题描述：
给定一个区间的集合，找到需要移除区间的最小数量，使剩余区间互不重叠。

注意:
可以认为区间的终点总是大于它的起点。
区间 [1,2] 和 [2,3] 的边界相互“接触”，但没有相互重叠。
贪心策略：
法一：与上题活动选择类似，用总区间数减去最大可同时进行的区间数即为结果。
法二： 当按照起点先后顺序考虑区间时，利用一个prev指针追踪刚刚添加到最终列表中的区间。遍历时，可能遇到三种情况：
情况1：当前考虑的两个区间不重叠。这种情况下不移除任何区间，将prev赋值为后面的区间，移除区间数量不变。

情况2：两个区间重叠，后一个区间的终点在前一个区间的终点之前。由于后一个区间的长度更小，可以留下更多空间，容纳更多区间，将prev更新为当前区间，移除区间的数量+1

情况3：两个区间重叠，后一个区间的终点在前一个区间的终点之后。直接移除后一个区间，留下更多空间。因此，prev不变，移除区间的数量+1

代码实现： 法一：

struct cmp{
    bool operator()(vector<int>& s1, vector<int>& s2){
        return s1[1] < s2[1];
    }
};
class Solution {
public:
    int eraseOverlapIntervals(vector<vector<int>>& intervals) {
        sort(intervals.begin(), intervals.end(), cmp());
        int num = 1;
        int i = 0;
        for(int j = 1; j < intervals.size(); j++){
            if(intervals[j][0] >= intervals[i][1]){
                i = j;
                num++;
            }
        }
        return intervals.size() - num;
    }
};

法二：

struct cmp{
    bool operator()(vector<int>& s1, vector<int>& s2){
        return s1[1] < s2[1];
    }
};
class Solution {
public:
    int eraseOverlapIntervals(vector<vector<int>>& intervals) {
        if(intervals.empty())
            return 0;
        sort(intervals.begin(), intervals.end(), cmp());
        int prev = 0;
        int num = 0;
        for(int i = 1; i < intervals.size(); i++){
            //情况1 不冲突
            if(intervals[i][0] >= intervals[prev][1]){
                prev = i;
            }else{
                if(intervals[i][1] < intervals[prev][1]){
                    //情况2
                    prev = i;
                }
                num++;
            }
        }
        return num;
    }
};