二叉树基础算法

发表于 2018-12-27 分类于算法

二叉树题目的递归解法可以分两类思路，第一类是遍历一遍二叉树得出答案，第二类是通过分解问题计算出答案，这两类思路分别对应着回溯算法核心框架和动态规划核心框架。

示例一：二叉树的最大深度

题面描述

给定一个二叉树，找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。

示例：
给定二叉树 [3,9,20,null,null,15,7]，

返回它的最大深度 3 。

题目解析

这题的思路是什么？显然遍历一遍二叉树，用一个外部变量记录每个节点所在的深度，取最大值就可以得到最大深度，这就是遍历二叉树计算答案的思路。
解法代码如下：

// 记录最大深度
int res = 0;
// 记录遍历到的节点的深度
int depth = 0;

// 主函数
int maxDepth(TreeNode root) {
	traverse(root);
	return res;
}

// 二叉树遍历框架
void traverse(TreeNode root) {
	if (root == null) {
		return;
	}
	// 前序位置
	depth++;
    if (root.left == null && root.right == null) {
        // 到达叶子节点，更新最大深度
		res = Math.max(res, depth);
    }
	traverse(root.left);
	traverse(root.right);
	// 后序位置
	depth--;
}

这个解法应该很好理解，但为什么需要在前序位置增加 depth，在后序位置减小 depth？
因为前面说了，前序位置是进入一个节点的时候，后序位置是离开一个节点的时候，depth 记录当前递归到的节点深度，你把 traverse 理解成在二叉树上游走的一个指针，所以当然要这样维护。
至于对 res 的更新，你放到前中后序位置都可以，只要保证在进入节点之后，离开节点之前（即 depth 自增之后，自减之前）就行了。
当然，你也很容易发现一棵二叉树的最大深度可以通过子树的最大深度推导出来，这就是分解问题计算答案的思路。

解法代码如下：

// 定义：输入根节点，返回这棵二叉树的最大深度
int maxDepth(TreeNode root) {
	if (root == null) {
		return 0;
	}
	// 利用定义，计算左右子树的最大深度
	int leftMax = maxDepth(root.left);
	int rightMax = maxDepth(root.right);
	// 整棵树的最大深度等于左右子树的最大深度取最大值，
    // 然后再加上根节点自己
	int res = Math.max(leftMax, rightMax) + 1;

	return res;
}

只要明确递归函数的定义，这个解法也不难理解，但为什么主要的代码逻辑集中在后序位置？
因为这个思路正确的核心在于，你确实可以通过子树的最大深度推导出原树的深度，所以当然要首先利用递归函数的定义算出左右子树的最大深度，然后推出原树的最大深度，主要逻辑自然放在后序位置。

示例二：二叉树的直径

题面描述

给定一棵二叉树，你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过也可能不穿过根结点。

示例 :
给定二叉树

返回 3, 它的长度是路径 [4,2,1,3] 或者 [5,2,1,3]。

注意：两结点之间的路径长度是以它们之间边的数目表示。

题目解析

所谓二叉树的「直径」长度，就是任意两个结点之间的路径长度。最长「直径」并不一定要穿过根结点，比如上面这棵二叉树，它的最长直径是 [4,2,1,3] 或者 [5,2,1,3]。
解决这题的关键在于，每一条二叉树的「直径」长度，就是一个节点的左右子树的最大深度之和。
现在让我求整棵树中的最长「直径」，那直截了当的思路就是遍历整棵树中的每个节点，然后通过每个节点的左右子树的最大深度算出每个节点的「直径」，最后把所有「直径」求个最大值即可。
最大深度的算法我们刚才实现过了，上述思路就可以写出以下代码：

// 记录最大直径的长度
int maxDiameter = 0;

public int diameterOfBinaryTree(TreeNode root) {
    // 对每个节点计算直径，求最大直径
    traverse(root);
    return maxDiameter;
}

// 遍历二叉树
void traverse(TreeNode root) {
    if (root == null) {
        return;
    }
    // 对每个节点计算直径
    int leftMax = maxDepth(root.left);
    int rightMax = maxDepth(root.right);
    int myDiameter = leftMax + rightMax;
    // 更新全局最大直径
    maxDiameter = Math.max(maxDiameter, myDiameter);
    
    traverse(root.left);
    traverse(root.right);
}

// 计算二叉树的最大深度
int maxDepth(TreeNode root) {
    if (root == null) {
        return 0;
    }
    int leftMax = maxDepth(root.left);
    int rightMax = maxDepth(root.right);
    return 1 + Math.max(leftMax, rightMax);
}

这个解法是正确的，但是运行时间很长，原因也很明显，traverse 遍历每个节点的时候还会调用递归函数 maxDepth，而 maxDepth 是要遍历子树的所有节点的，所以最坏时间复杂度是 O(N^2)。
这就出现了刚才探讨的情况，前序位置无法获取子树信息，所以只能让每个节点调用 maxDepth 函数去算子树的深度。
那如何优化？我们应该把计算「直径」的逻辑放在后序位置，准确说应该是放在 maxDepth 的后序位置，因为 maxDepth 的后序位置是知道左右子树的最大深度的。
所以，稍微改一下代码逻辑即可得到更好的解法：

// 记录最大直径的长度
static int maxDiameter = 0;
public static int diameterOfBinaryTree(TreeNode root) {
    maxDepth(root);
    return maxDiameter;
}
private static int maxDepth(TreeNode root){
    if(root==null)
        return 0;
    int leftMax = maxDepth(root.left);
    int rightMax = maxDepth(root.right);
    // 后序位置，顺便计算最大直径
    maxDiameter = Math.max(maxDiameter, leftMax + rightMax);
    return Math.max(leftMax ,rightMax) + 1;
}

这下时间复杂度只有 maxDepth 函数的 O(N) 了。

示例三：在每个树行中找最大值

题面描述

给定一棵二叉树的根节点 root ，请找出该二叉树中每一层的最大值。

示例1：

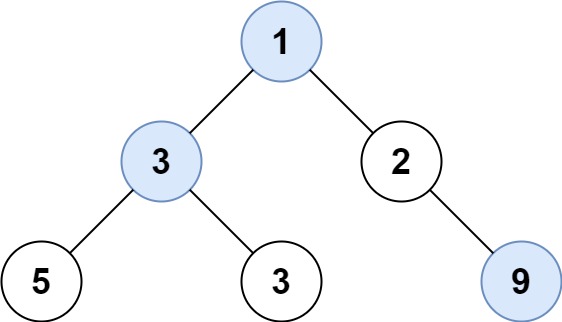
输入: root = [1,3,2,5,3,null,9]
输出: [1,3,9]
示例2：

输入: root = [1,2,3]
输出: [1,3]

提示：
二叉树的节点个数的范围是 [0,10^4]
-2^31 <= Node.val <= 2^31 - 1

题目解析

既然是找每一层中的最大值，那就必须执行过程中树的每层数据是清晰明了的，然后找出最大值。

这就要说一下二叉树的层序遍历了，而层序遍历属于迭代遍历，也比较简单，代码如下：

public static void levelTraverse(TreeNode root) {
    if(root==null)
        return;
    Queue<TreeNode> queue = new LinkedList<>();
    queue.offer(root);
    // 从上到下遍历二叉树的每一层
    while (!queue.isEmpty()){
        int size = queue.size();
        // 从左到右遍历每一层的每个节点
        for(int i=0;i<size;i++){
            TreeNode poll = queue.poll();
            System.out.print(poll.val + " ");
            // 将下一层节点放入队列
            if(poll.left!=null)
                queue.offer(poll.left);
            if(poll.right!=null)
                queue.offer(poll.right);
        }
    }
    println("");
}

这里面 while 循环和 for 循环分管从上到下和从左到右的遍历：

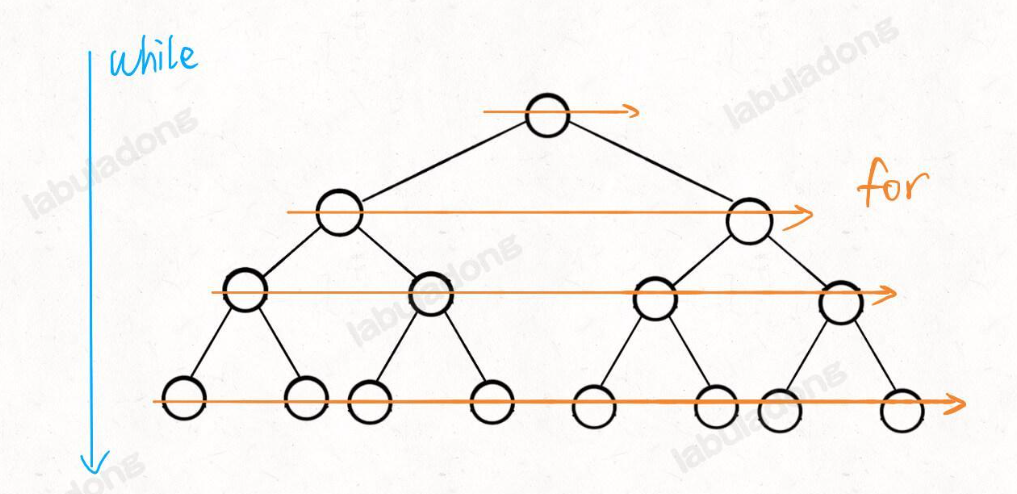
层序遍历搞清楚后，那上面的问题就好处理了，只需要找出每层的最大值即可，代码如下：

public static List<Integer> largestValues(TreeNode root) {
    if(root==null)
        return null;
    List<Integer> result = new ArrayList<>();
    Queue<TreeNode> queue = new LinkedList<>();
    queue.offer(root);
    // 从上到下遍历二叉树的每一层
    while (!queue.isEmpty()){
        int size = queue.size();
        int max = queue.peek().val;
        // 从左到右遍历每一层的每个节点
        for(int i=0;i<size;i++){
            TreeNode poll = queue.poll();
            //更新最大值
            max = Math.max(max, poll.val);
            // 将下一层节点放入队列
            if(poll.left!=null)
                queue.offer(poll.left);
            if(poll.right!=null)
                queue.offer(poll.right);
        }
        result.add(max);
    }
    return result;
}